Functions visualized with pretty circles

To pack a space with circles means to put circles in it so that if you were to enlarge any of them they would overlap.
It's a simple concept, but I believe it has many interesting applications for games and art. Transforming photos into the "circle style" has been done a lot. I haven't seen it used for abstract ("mathematical") art or world generation, though.
Demo time
Before diving into more details I'll show you a simple demo of what circle packing may look like.
I've coded this in vanilla JavaScript while experimenting. It animates circle packing based on provided mathematical formula. Go ahead and click the buttons to see it come alive.
I know the "Christmas tree" is sideways, but you can just tilt your head and pretend it's fine.
If you are reading this article on your computer feel free to open the developer console and call the demoCtrl.run() function. A few examples you can try:
// Mountains
demoCtrl.run(x => Math.sin(x) * Math.cos(x/3), 'y = sin(x) * cos(x/3)')
// Spiral
demoCtrl.run(x => x / 30, 'r = α / 30', { circular: true, color: 'white', bgColor: 'green' })
The demo
The source code is available here. Don't expect anything fancy, though. It's just a quick prototype taking up less than 200 lines.
Basic algorithm
The idea is to spawn circles randomly on the screen and then gradually increase their size. A circle stops growing when it collides with another circle or a screen edge.
In my case I spawn up to 20 circles every frame and grow their radiuses (or radii) uniformly by 20 pixels per second. Also, instead of placing them fully randomly, I do the following:
- gradually increase the x coordinate over time (5 pixels per second)
- calculate the y coordinate based on some function taking x as input
And on top of that I add a little random variation to the position of each circle (+ 0-25 pixels for each coordinate).
Circle out of circles
Of course, for the circular effect (like the Flower and Sun examples in the demo), the position algorithm is slightly different. Instead of increasing x over time, the angle is increased instead. Drawing the circles along a normal circle then looks like this:
x = centerX + radius * Math.cos(angle)
y = centerY + radius * Math.sin(angle)

To get the desired effect we can adjust the radius based on some function taking the angle as input (same as the y coordinate before).
const adjustedR = radius * someFunc(angle)
x = centerX + adjustedR * Math.cos(angle)
y = centerY + adjustedR * Math.sin(angle)

This looks nice already. To get the same effect as in the demo, just add some random variation:
x += Math.random() * randFactor
y += Math.random() * randFactor

Performance
While writing the demo I stumbled upon some animation performance issues. They were caused by drawing a lot of strokes (in circle form) on the canvas. Probably the best way to resolve them would be to use WebGL instead. I didn't, though, and tried to be smart about using the canvas.
The first idea I had was to redraw only the part of the canvas to the right from the last circle that's still growing. This means I wouldn't clear and redraw most of the circles that are not changing anymore.
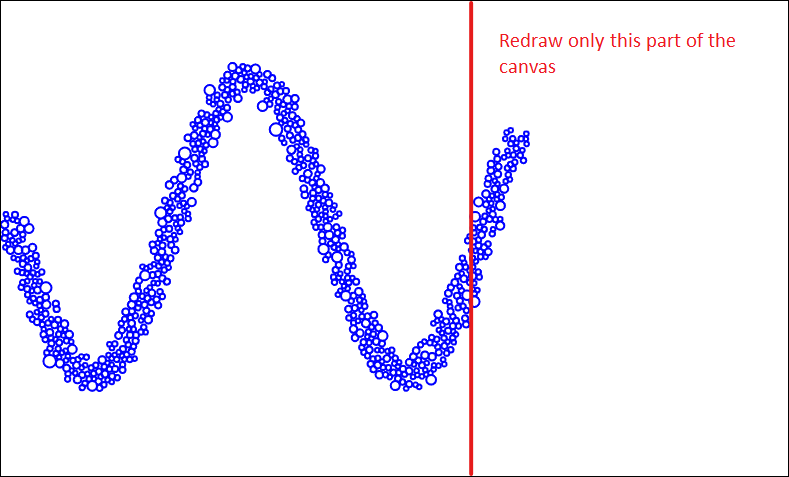
This worked. But only for the "increasing x coordinate over time" version of the algorithm. It's tricky to detect which parts of the canvas to redraw in the circular version.
Finally, I decided not to clear the canvas at all.
Instead, every frame the circles that are still growing get covered by background colored circles. Only then newly grown circles are drawn again. This way only the pixels that actually changed are redrawn. It turned out to be efficient enough for my needs (that is - runs smoothly on my phone).
Collision checks
Also, note that checking which circles are blocked can potentially be a performance bottleneck. To check for collisions you have to check every circle against every other circle. If there are 1000 circles you'll end up with 1,000,000 checks every frame.
The simplest way to mitigate it is to mark the blocked circles as such so they are not checked again. I also store them in a separate array so the algorithm doesn't need to iterate over the blocked circles when only growing ones are needed. Assuming there are 1000 circles but only 50 of them are growing - this gives us 50,000 checks every frame. A lot better.
If not for the circular version of the animation, old circles could even be removed from memory entirely. That's because there isn't a need to check for collision with them and they're drawn to the screen already.

Other application
I tried to think of other ways to utilize circle packing. Math animations are cool but could it be used for procedural world generation? This is what i came up with:
Spawn circles randomly until some percent of space is filled and create a world map with properties such as elevation, biomes, oceans, cities, etc based on:
- circle density in a given area
- whether a point is inside a circle or not
- how many other circles a given circle collides with
- the distance to the biggest and/or smallest circle on the map
- and possibly other properties
Having proposed that, this deserves an article on its own. Let me know what you think. Maybe I'll explore this idea further. Stay tuned and join my mailing list if you like this kind of stuff and would like to be notified about new articles.